Учебные пособия > College Algebra
Now that we have analyzed the equations for rational functions and how they relate to a graph of the function, we can use information given by a graph to write the function. A rational function written in factored form will have an x-intercept where each factor of the numerator is equal to zero. (An exception occurs in the case of a removable discontinuity.) As a result, we can form a numerator of a function whose graph will pass through a set of x-intercepts by introducing a corresponding set of factors. Likewise, because the function will have a vertical asymptote where each factor of the denominator is equal to zero, we can form a denominator that will produce the vertical asymptotes by introducing a corresponding set of factors.
A General Note: Writing Rational Functions from Intercepts and Asymptotes
If a rational function has x-intercepts at [latex]x=_, _, . _[/latex], vertical asymptotes at [latex]x=_,_,\dots ,_[/latex], and no [latex]_=\text_[/latex], then the function can be written in the form: [latex]f\left(x\right)=a\frac<<\left(x-_\right)>^_><\left(x-_\right)>^_>\cdots <\left(x-_\right)>^_>><<\left(x-_\right)>^_><\left(x-_\right)>^_>\cdots <\left(x-_\right)>^_>>[/latex] where the powers [latex]_[/latex] or [latex]_[/latex] on each factor can be determined by the behavior of the graph at the corresponding intercept or asymptote, and the stretch factor a can be determined given a value of the function other than the x-intercept or by the horizontal asymptote if it is nonzero.
How To: Given a graph of a rational function, write the function.
- Determine the factors of the numerator. Examine the behavior of the graph at the x-intercepts to determine the zeroes and their multiplicities. (This is easy to do when finding the "simplest" function with small multiplicities—such as 1 or 3—but may be difficult for larger multiplicities—such as 5 or 7, for example.)
- Determine the factors of the denominator. Examine the behavior on both sides of each vertical asymptote to determine the factors and their powers.
- Use any clear point on the graph to find the stretch factor.
Example: Writing a Rational Function from Intercepts and Asymptotes
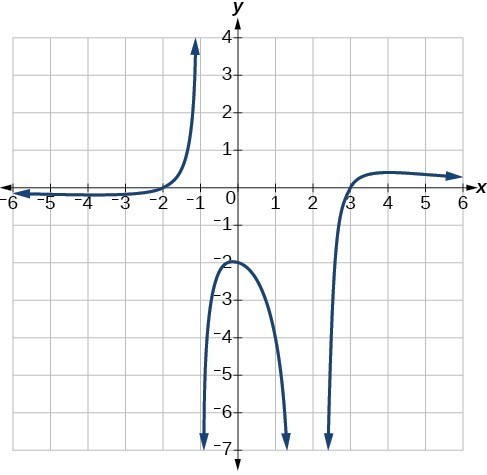
Write an equation for the rational function below.

Answer: The graph appears to have x-intercepts at [latex]x=-2[/latex] and [latex]x=3[/latex]. At both, the graph passes through the intercept, suggesting linear factors. The graph has two vertical asymptotes. The one at [latex]x=-1[/latex] seems to exhibit the basic behavior similar to [latex]\frac[/latex], with the graph heading toward positive infinity on one side and heading toward negative infinity on the other. The asymptote at [latex]x=2[/latex] is exhibiting a behavior similar to [latex]\frac<^>[/latex], with the graph heading toward negative infinity on both sides of the asymptote. We can use this information to write a function of the form
To find the stretch factor, we can use another clear point on the graph, such as the y-intercept [latex]\left(0,-2\right)[/latex].
Key Equations
| Rational Function | [latex]f\left(x\right)=\frac=\frac^ +_ ^ +. +_x+_>_^+_^+. +_x+_>, Q\left(x\right)\ne 0[/latex] |
Key Concepts
- We can use arrow notation to describe local behavior and end behavior of the toolkit functions [latex]f\left(x\right)=\frac[/latex] and [latex]f\left(x\right)=\frac<^>[/latex].
- A function that levels off at a horizontal value has a horizontal asymptote. A function can have more than one vertical asymptote.
- Application problems involving rates and concentrations often involve rational functions.
- The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.
- The vertical asymptotes of a rational function will occur where the denominator of the function is equal to zero and the numerator is not zero.
- A removable discontinuity might occur in the graph of a rational function if an input causes both numerator and denominator to be zero.
- A rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.
- Graph rational functions by finding the intercepts, behavior at the intercepts and asymptotes, and end behavior.
- If a rational function has x-intercepts at [latex]x=_,_,\dots ,_[/latex], vertical asymptotes at [latex]x=_,_,\dots ,_[/latex], and no [latex]_=\text_[/latex], then the function can be written in the form [latex]f\left(x\right)=a\frac<<\left(x-_\right)>^_><\left(x-_\right)>^_>\cdots <\left(x-_\right)>^_>><<\left(x-_\right)>^_><\left(x-_\right)>^_>\cdots <\left(x-_\right)>^_>>[/latex]
Glossary
arrow notation a way to symbolically represent the local and end behavior of a function by using arrows to indicate that an input or output approaches a value horizontal asymptote a horizontal line y = b where the graph approaches the line as the inputs increase or decrease without bound. rational function a function that can be written as the ratio of two polynomials removable discontinuity a single point at which a function is undefined that, if filled in, would make the function continuous; it appears as a hole on the graph of a function vertical asymptote a vertical line x = a where the graph tends toward positive or negative infinity as the inputs approach a
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License:CC BY: Attribution.
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License:CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License:CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 129042, 129067, 129072, 129075. Authored by: Alyson Day. License:CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 74565. Authored by: Nearing, Daniel, mb Lippman, David. License:CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Ex: The Domain of Rational Functions . Authored by: James Sousa (Mathispower4u.com) . License:CC BY: Attribution.
- Question ID 105058. Authored by: Jim Smart. License:CC BY: Attribution. License terms: IMathAS Community License, CC-BY + GPL.
- Question ID 15836. Authored by: James Sousa . License:CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Ex: Determine Horizontal Asymptotes of Rational Functions . Authored by: James Sousa (Mathispower4u.com) . License:CC BY: Attribution.
- Ex: Find the Intercepts, Asymptotes, and Hole of a Rational Function . Authored by: James Sousa (Mathispower4u.com) . License:CC BY: Attribution.
- Question ID 1802. Authored by: Lippman, David. License:CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Ex: Match Equations of Rational Functions to Graphs . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License:CC BY: Attribution.



